3-Dimensional Moire Patterns
Regular Nested Rotational Symmetries
2- and 3-dimensional self-similarity and synchronicity in Platonic dipolygonoid geometry
Prithvi Rana Dev
2023
Abstract — An exploration of moving-image interference using Fuller-Stuart-Clinton dipolygonoids reveals a series of 3-dimensional moire patterns that exhibit regularity. These modular kinetics extend synchronicity from 2- dimensional periodicity to 3-dimensions. Elements of a platonic structure are self-similar, constructed with only one type of regular polygon i.e, the equilateral triangle (for tetra-, octa-, and icosahedral transformers), squares (for the cube transformer), and pentagons (for the dodecahedron transformer). Each jitterbug face consists of 2 identical overlapping polygons i.e, a dipolygon. Dipolygons are superimposed with identical periodic or quasi-periodic grids (3-, 4-, or 5-gon lattices) which create self-similar interference patterns as each structure unfolds. Rotation-translation along every dipolygon axis results in a chiral ex- and impansion of each platonic dipolyhedron, with equivalent rotational periods in 2-dimensional moire and 3-dimensional motion. The result is a set of scale-independent and multi-dimensional structures that perform multiple symmetry operations at once. I present this set of regular symmetries with relevant observations, further extensions in reasoning, as well as my process of construction.
I. INTRODUCTION
The Rhode Island School of Design’s nature lab houses a curious collection of physical models and toys called the Loeb collection. This was my first exposure to the themes and ideas that shaped the work presented in this paper. Collated by the crystallographer and geometrician Arthur Loeb, its many fascinating objects help intuit structure from the micro and molecular to the macro and cosmic scales of the universe. 2-d tessellation prints and 3-d models such as Buckminster Fuller’s jitterbug and other tensegrity models underline the core principles of pattern, symmetry, and structure that nature employs to build our reality.
Fuller’s iconic jitterbug inspired the design-scientists R. Duncan Stuart, Joseph D. Clinton, and H.F. Verheyen to make and describe a class of expanding-contracting structures called dipolygonoids. These handheld architectural models delight through radial and cyclic movement. Rivets at the center of each face create rotational pivots, while vertex-to-vertex connections between inside and outside layers of adjacent faces provide tensile strength with continuous elasticity. Together they over-constrain each structure’s spatial mechanics. Binary interconnectivity permits rotation-translation, revealing a sequence of nested alterations to regular Platonic and semi-regular Archimedean solids. This kinematic provides a visual approach to understand and construct uniform polyhedra using geometric duality in their 3-dimensional shape.
Interference is a function of motion in semi-tensile dipolygonoids. Overlapping polygons require time to rotate in opposite directions, allowing dipolygons the potential to animate. Novel experiments with this concept involve a material adjustment - constructing modules using graphic sticker-transparencies and acrylic sheets. This allows analog illusion and moving-image techniques that employ dot and line patterns, cut- outs, colour, opacity, and many other visual tools. When regularity is considered, 3- and 4-fold lattices are applied to 3- and 4-polygons and their corresponding regular dipolygonoids, whereas 5- fold quasi-periodic patterns build on the 5-fold symmetry of the dodecahedral dipolygonoid. Resultant self-similarity in structure, grid, and interference lends periodic harmony to elements in transformation.
First we understand regular structures in 2-dimensions and the tessellations that arise from these. Then we see self-similar interference patterns arising from 2-dimensional regular and quasi-periodic tessellations. We then explore 3-dimensional regularity in the platonic solids, the jitterbug, dipolygonoids, and describe self-similar 3-dimensional patterns which constitute multiple symmetry operations simultaneously. Physical constructions of such structures shall be discussed. Finally, we visit mathematical chiral transformations in 3-dimensions and extend this reasoning into higher dimensions as well.
II. REGULAR SHAPES AND TESSELLATIONS IN 2-DIMENSIONS
i. Regular polygons
A regular polygon is a 2-dimensional n-sided shape in which the sides are all the same length and are symmetrically placed about a common center, i.e., the polygon is both equiangular and equilateral. The terms equilateral triangle and square refer to the regular 3- and 4-polygons. Pentagons are regular 5- polygons, third in an infinite series of perfect polygonal shapes in 2-dimensions that approximate to a circle at infinity (Fig.1).
The equilateral triangle or 3-polygon (Fig.2), consists of 3 equal length sides at 60-degree adjacent angles from one-another. These lines meet at 3 vertices, A, B, and C, which are equidistant from center O (Fig.3). The triangle repeats itself i.e, translates, with every 120-degree rotation through axis O, creating 3 instances of symmetry through 360-degrees.
The square or 4-polygon (Fig.4) has 4 equal length sides at a 90-degree right angle from one-another, and the pentagon or 5-polygon (Fig.6) has 108- degree angles between 5 equal length sides. Squares have 4 vertices, A, B, C, and D (Fig.5), and pentagons have 5 vertices, A, B, C, D, and E (Fig.7) - that are each equidistant from center O. Squares repeat with every 90-degree rotation pivoted at O, having 4 instances of symmetry in 360-degrees. A pentagon requires 72-degree rotations for 5 symmetric repetitions through 360- degrees.
Hence the equilateral triangle exhibits 3-fold symmetry, while squares and pentagons exhibit 4- and 5-fold symmetry, respectively.
Fig.1
Infinite series of regular 2D polygons
Fig.2
Equilateral Triangle (3-Polygon)
Fig.3
Symmetries of the Equilateral Triangle
Fig.4
Square (4-Polygon)
Fig.5
Symmetries of the Square
Fig.6
Pentagon (5-Polygon)
Fig.7
Symmetries of the Pentagon
ii. Regular tessellations
A tessellation is a pattern of shapes repeated to fill a plane or space. These can be a tiling of polygons (2-dimensional), polyhedra (3-dimensional), or polytopes (n-dimensional).
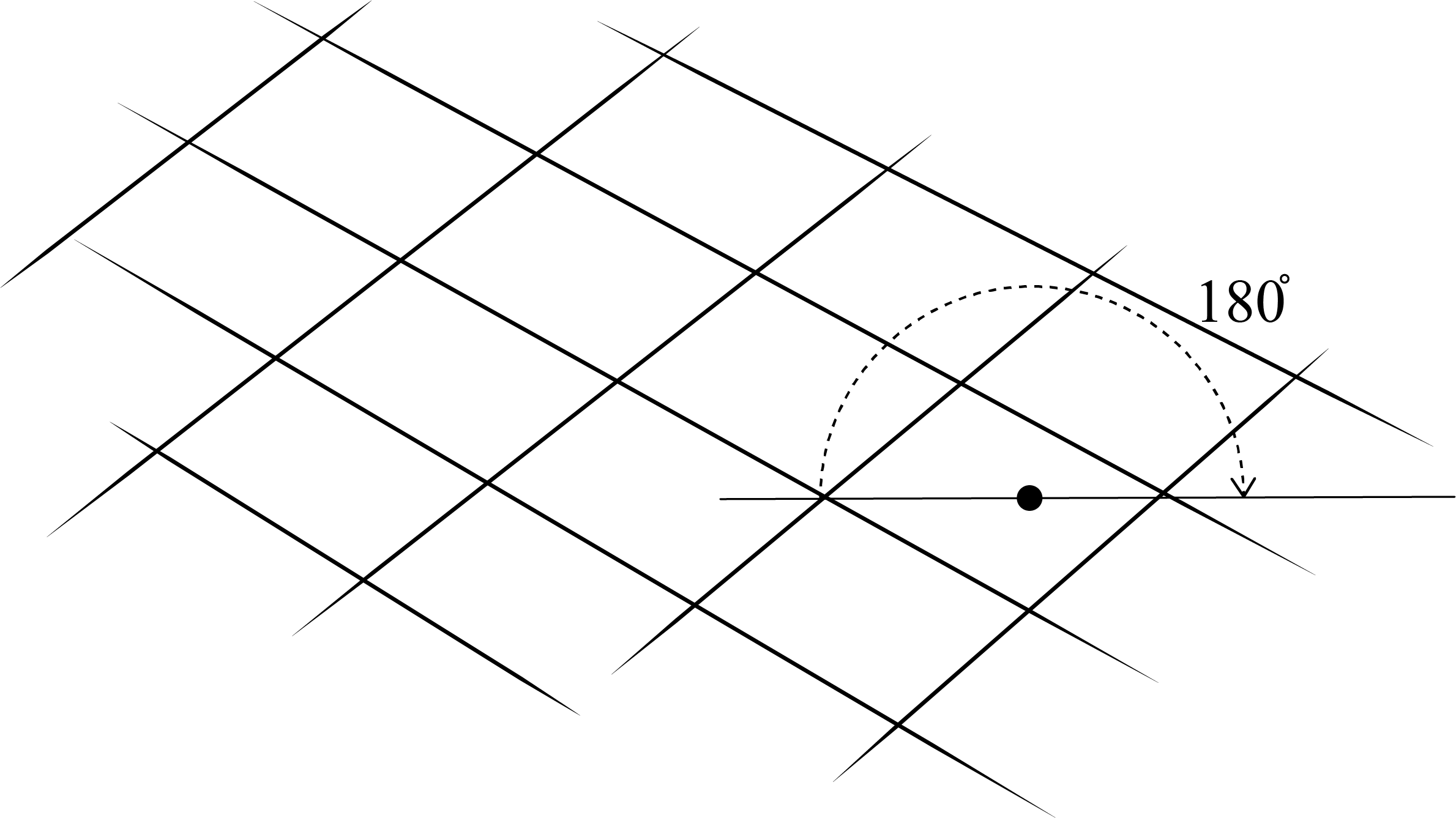
In 2-dimensions, the breaking up of self- intersecting polygons into simple polygons is also called a tessellation, or more properly, a polygon tessellation. The shapes do not overlap and there are no gaps. For a tessellation made of polygons, the sum of angles formed at any vertex is 360 degrees. For example, a congruent polygon tessellation is made of parallelograms (2-fold, Fig.8), which has a rotation-translation of 180 degrees.
A regular tessellation is made up of only one type of regular polygon. They are highly symmetric edge to edge tilings that can theoretically fill a plane to infinity. There are only 3 tessellations that are composed entirely of regular polygons, those made of equilateral triangles (3-fold, Fig.9), squares (4-fold, Fig.10), and hexagons (6-fold, Fig.11). Each of them have rotational-translational symmetry. The 3-fold tessellation translates at 120 degrees, 4-fold at 90 degrees, and 6-fold at 60 degrees of rotation.
In 3-dimensions, a polyhedron which is capable of tessellating space is called a space-filling polyhedron. Examples include the cube, rhombic dodecahedron, and truncated octahedron. A tessellation of n-dimensional polytopes is called a honeycomb lattice.
Fig.8
2-fold tessellation
Fig.9
3-fold tessellation
Fig.10
4-fold tessellation
Fig.11
6-fold tessellation
When a polygon structure and superimposed tessellation are constructed with the same n-fold symmetry, they create self-similar modules. Seen below (Fig.12) are wireframe self-similar 3- and 4-fold modules.
Fig.12
Self-similarity : wireframe 3- and 4-tessellations superimposed on 3- and 4-polygons
When dipolygons (2 overlapping layers of identical regular polygons) are considered in the construction of platonic dipolygonoids, checkered (black and transparent) tessellations create a relevant superimposition for self-similarity (Fig.13, Fig.14). As these alternately checkered grids perfectly overlap, the structure becomes opaque, because the transparent polygons of the top layer grid overlap with the black polygons on the bottom layer grid.
Fig.13
Checkered 3-fold self-similar module and its alternate
Fig.14
Checkered 4-fold self-similar module and its alternate
Parallelograms and hexagons do not make any regular 3-dimensional solid. So we shall consider only equilateral triangle and square tessellations for the construction of Platonic dipolygonoids. This is because in terms of regularity, only 3-fold and 4- fold tessellations create appropriate superimpositions for a self-similar module.
iii. Quasi-periodic tessellations
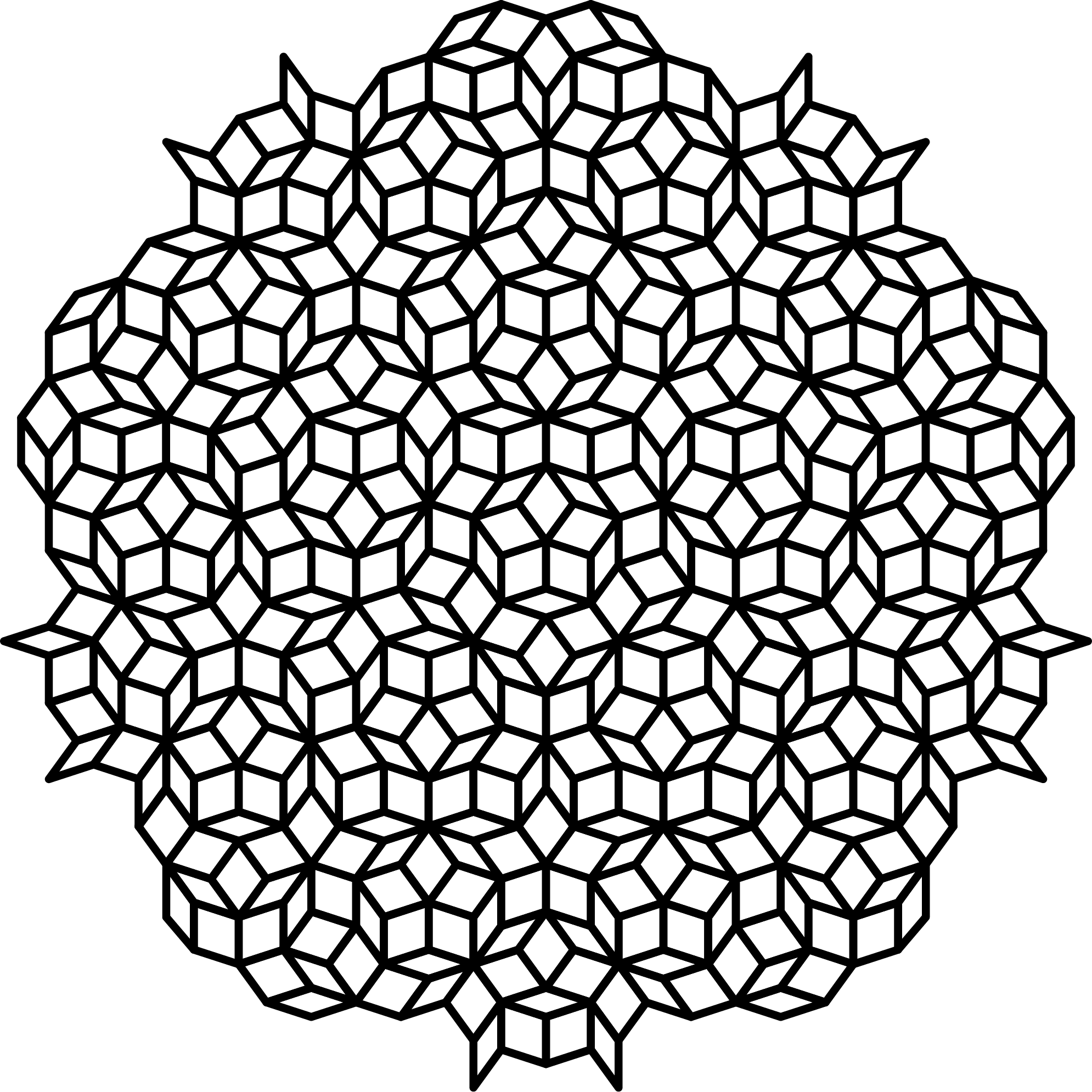
The discovery of quasicrystals (Fig.15) by Dan Shechtman in 1982 led to a redefinition of symmetries to include quasi-periodic 5-fold symmetry (as well as 8, 10 and 12-fold), to the existing 2-, 3-, 4- and 6-fold symmetry system of crystallography as exhibited in natural crystals. Previously in the 1960's, Roger Penrose created aperiodic tilings now known as Penrose tilings (Fig.16), which had quasicrystalline symmetry. Shechtman's discovery was the first instance of them being found in nature.
They are termed ‘quasi’ because their molecular arrangements are ordered but not periodic, in the sense you can continuously fill all available space using the pattern, but the atomic lattice lacks translational symmetry. This means a shifted copy will never match the original, or that they exhibit incommensurability along any given direction. They cannot be periodically tiled, for instance, the way a square grid or cubic lattice can. In theory they can be viewed as irrational 3-dimensional slices of hyper-cubic 5-dimensional or higher dimensional periodic lattices (sliced at ~1.618 degrees), that are then projected with an icosahedral perspective onto 2 dimensions to create quasi-periodic dot arrangements (Fig.17, Fig.18).
These provide 5-fold pentagonal symmetry with which we can create a rotation-translation interference pattern while staying true to the 5-fold symmetry of the dodecahedron, thus allowing for self-similar dodecahedral dipolygonoids.
Fig.15
Shechtman’s x-ray diffraction of the Al86Mn14 alloy : 10-fold quasi-periodic pattern
Fig.16
Penrose tiling : 5-fold symmetry
Fig.17
8-fold and 12-fold diffraction patterns
Fig.18
Self-similarity : 5-fold icosahedral projection of a quasicrystal on a 5-polygon
III. SELF-SIMILAR 2-DIMENSIONAL MOIRE PATTERNS
i. Regular interferences
An interference pattern occurs when two waves superpose to form a resultant wave of greater, lower, or the same amplitude. It can be visually created by overlapping grids (lattices) or dot arrangements, and is produced when an opaque regular pattern with transparent gaps is overlaid on another similar pattern. These appear only when the patterns are rotated by a small twist angle relative to each other or have different, but similar pitches.
Moire emerges from the superimposition and slight miss registration of two or more patterns. A classic moire is composed of two sets of parallel lines that are at a slight angle, but moire patterns can also develop out of grids or dot arrays, curved lines, and innumerable other arrangements. Jennifer L. Roberts states that the key quality of a moire pattern is that it emerges in a nonlinear way from its component structures. It does not exist in either individual pattern but is generated only in their combination. Depending on the mutual angles, frequencies, and periodicities of the two elements, moire can crop up in a lot of different places. It explores an intersubjective neurological space, a space of intermediation. Yet it is an objective phenomenon as it operates in the oral register as well, through cymatic patterns and beat phenomenon. Frequencies of sound can generate moire beats as the sound is unfolding.
Moire patterns create a tension between bottom-up or physical signals, and top-down or cognitive signals. The interference of these lines, grids, and dots that the brain or a machine registers, adds up adjacent areas in the retina to create the illusory optical pattern. It is a self-generated illusion who’s mechanisms of creation are absolutely obvious, as there’s no sleeves, smoke, or mirrors.
A regular moire pattern consists of an n-fold dipolygon, identical n-fold tessellations, and a resulting n-fold interference i.e, all components are self-similar, made of only one type of regular polygon. For example, a wireframe 3-fold tessellation superimposed on an equilateral triangle (with 120 degree translational symmetry) - rotated against an identical grid about a common center - will produce an interference of telescoping equilateral triangles with a periodicity or angle of symmetry of 120 degrees (Fig.19). The same is true for the wireframe 4-fold tessellation and square dipolygon (with 90 degree translational symmetry), from which a square moire pattern emerges with a periodicity of 90 degrees (Fig.20).
Fig.19
Sequence of self-similar 3-fold dipolygon, grids, and moire, with a periodicity of 120 degrees
Fig.20
Sequence of self-similar 4-fold dipolygon, grids, and moire, with a periodicity of 90 degrees
ii. Checkered interferences
If the 3-fold dipolygon tessellation consists of alternately checkered (black and transparent) triangles instead of wireframes, a very interesting interference with 360 degree periodicity occurs. The moire requires a full circle of rotation to overlap, and it’s animation of telescoping and magnifying regular polygons is 4-fold - square lines - with triangular vertices that are 90 degrees from the original grid (Fig.21).
When the 4-fold dipolygon tessellation consists of alternately checkered (black and transparent) squares instead of a wireframe grid, an interference with 180 degree periodicity occurs. While the grids are perfectly overlapped the dipolygon is opaque, and it requires half a circle of rotation to complete a moire cycle. The animation remains 4-fold - telescoping and magnifying squares with square vertices - at 45 degrees from the original grid, making it self-similar (Fig.22).
Fig.21
Sequence of a 3-fold dipolygon with alternately checkered 3-fold grids creates a 4-fold moire with a periodicity of 360 degrees
Fig.22
Sequence of a 4-fold dipolygon with alternately checkered 4-fold grids
Identically checkered 3-fold grids create a 3-fold moire with periodicity of 120 degrees. Initially one sees a telescoping pattern of white triangles with black grids. This inverts at 30 degrees to black triangles with white grids for a 60-degree sub-period - then reverts to the original pattern to complete the 120 degree cycle. Only by adding alternately checkered grids to the 3-fold dipolygons does the interference change to a 4-fold moire with a 360 degree cycle. Identically and alternately checkered 4-fold grids create a 4-fold moire perpendicular to the original grids with a periodicity of 180 degrees. Hence colouring in the tiles changes the algebraic relationships between interacting lines and shapes in 2-dimensional moire patterns.
Regular interferences have duality embedded in their motion. In each 2-dimensional moire we have observed so far, the pattern inverts or mirrors after a half cycle of its periodicity.
There is also a fractal-like nature to the dipolygons and the telescoping ghost patterns, in their nested quality. This arises from the equivalent rotation-translation periods of the two regular n-polygons and their n- fold tessellations i.e, in each pattern the structure, grid, and moire all obey the same n-fold symmetry, with the rotation cycle - R1, of the structure, and nested rotational period - R2, of the moire being synchronous.
iii. Quasi-interference patterns
The interference patterns of quasicrystals have circular symmetries embedded in their motion. These zoom radially inward and outward. There are 5 rotational-translational symmetries in the overall structural motion of the pentagonal dipolygon through 360 degrees. A self-similar 5-fold Penrose tiling and its resulting interference has 72 degree periodicity (Fig.23) whereas 10-fold quasicrystal interferences have 36 degree periodicity (Fig.24).
Fig.23
Sequence of a self-similar 5-fold dipolygon with Penrose tiling creates a 5-fold moire with periodicity of 72 degrees
Fig.24
Sequence of a 5-fold dipolygon with the 10-fold Al86Mn14 alloy creates a 10-fold moire with periodicity of 36 degrees
IV. REGULAR SHAPES IN 3-DIMENSIONS
A regular polyhedron is a 3-dimensional shape constructed with congruent (identical in shape and size), regular (all angles and sides equal) polygon faces, where the same number of faces meet at each vertex. Only 3 regular 2-dimensional polygons allow for the construction of regular 3-dimensional polyhedra - the 3-, 4-, and 5-polygon. At least 3 polygon faces meet at each vertex - where the internal angles must add up to less than 360 degrees - or the shape flattens out. There are 5 convex polyhedra that meet this criteria - the tetrahedron, octahedron and icosahedron (consisting of 4, 8, and 20 equilateral triangles respectively), the cube (6 squares), and the dodecahedron (12 pentagons). Collectively, they are the Platonic solids :
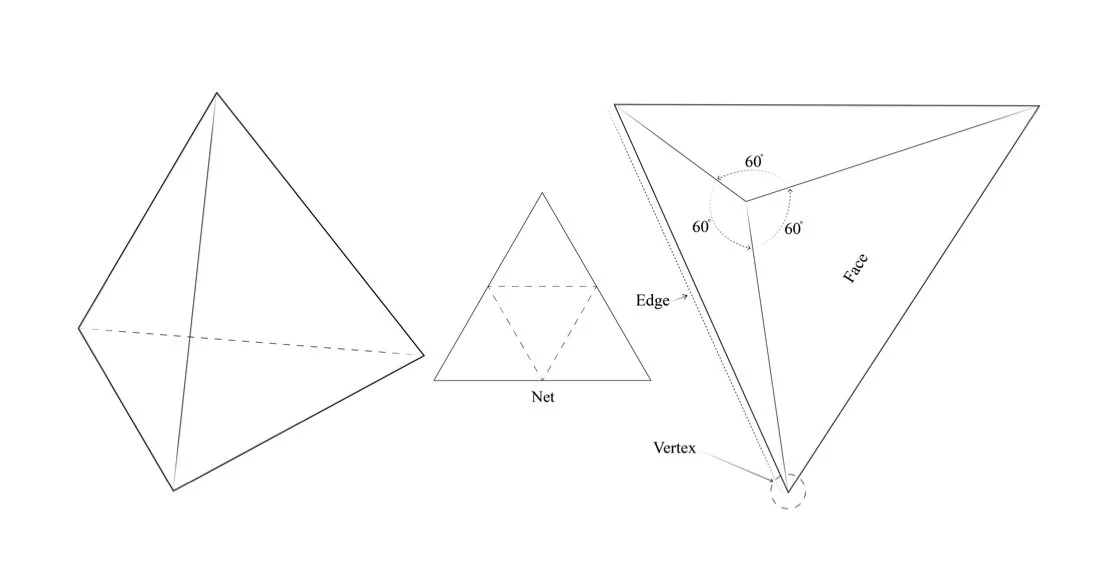
Tetrahedron :
The tetrahedron (Fig.25) or triangular pyramid is the simplest of the five Platonic solids. It consists of 4 equilateral triangle faces, creating 6 straight edges and 4 vertices - all of which are equidistant from each other. 3 triangles meet at each vertex with internal angles of 60 degrees, hence at each vertex the angles sum up to 180 degrees (60x3). It has a dihedral angle (face to face along an edge) of 70.529 degrees. Unlike other platonic solids, a tetrahedron has no parallel faces and it is also dual to itself.
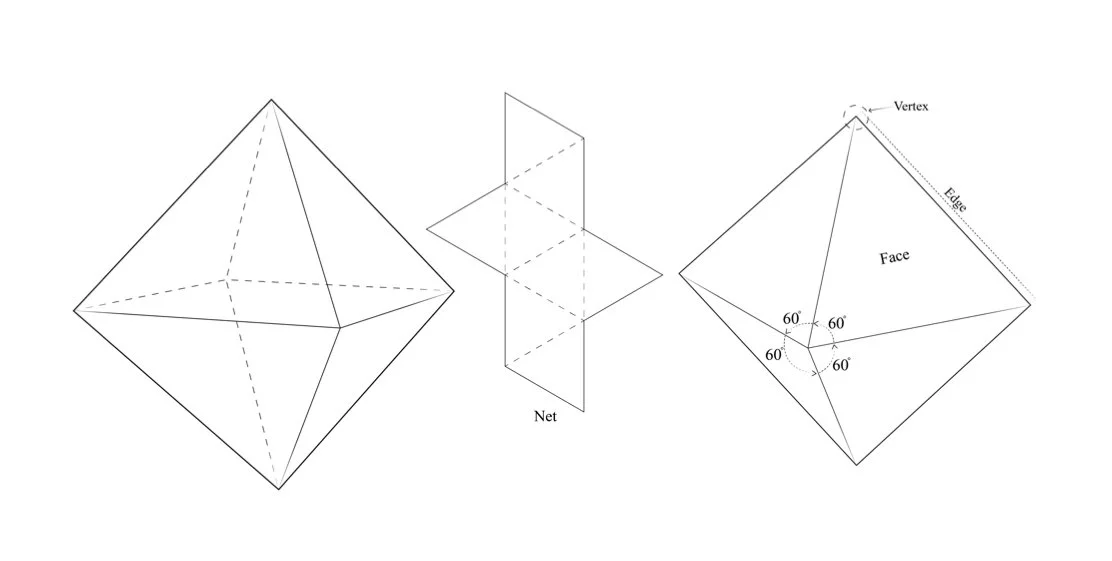
Octahedron :
The octahedron (Fig.26) is a polyhedron with 8 equilateral triangle faces, which creates 12 edges, and 6 vertices. 4 equilateral triangles meet at each vertex. The internal angles are 60 degrees, therefore the angles at each vertex sum up to 240 degrees (60x4). The dihedral angles are 109.471 degrees. The dual of the octahedron is the cube.
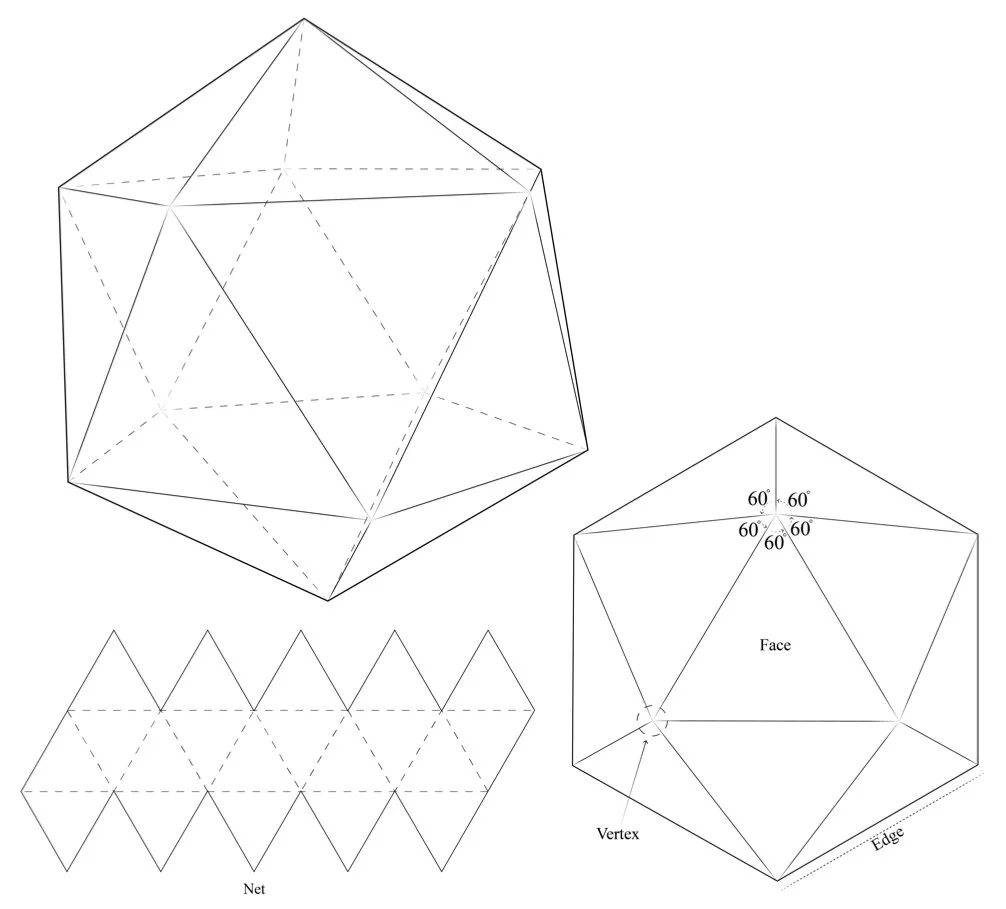
Icosahedron :
The icosahedron (Fig.27) has the most number of faces and the greatest volume for its surface area, of any platonic solid. It is often termed ‘the mathematician’s jewel’ for its beauty and symmetry. It consists of 20 equilateral triangle faces, which create 30 edges and 12 vertices. Since all internal angles are 60 degrees and 5 triangles meet at each vertex, the angles at each vertex sum up to 300 degrees (60x5). The dihedral angles are 138.189685 degrees. The dual of the icosahedron is the dodecahedron.
Fig.25
Tetrahedron
Fig.26
Octahedron
Fig.27
Icosahedron
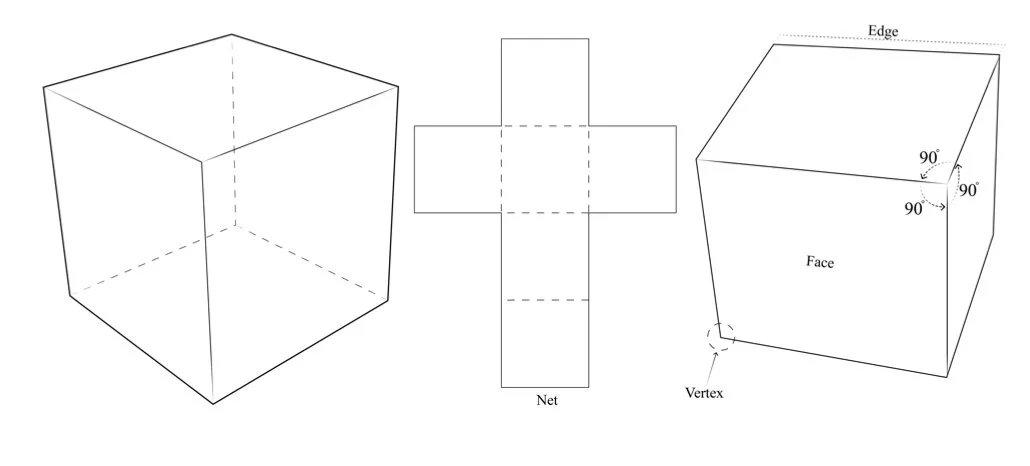
Cube :
A cube (Fig.28) or hexahedron is made of 6 square faces and all sides of the cube are the same length. It consists of 12 edges, 6 faces, and 8 vertices. Since cubes are made of congruent squares, the length, breath, and height of a cube are the same. The angles between any 2 faces or surfaces (internal and dihedral angles) is 90 degrees. 3 squares meet at each vertex, therefore the internal angles at each vertex add up to 270 degrees (90x3). The dual of the cube is the octahedron.
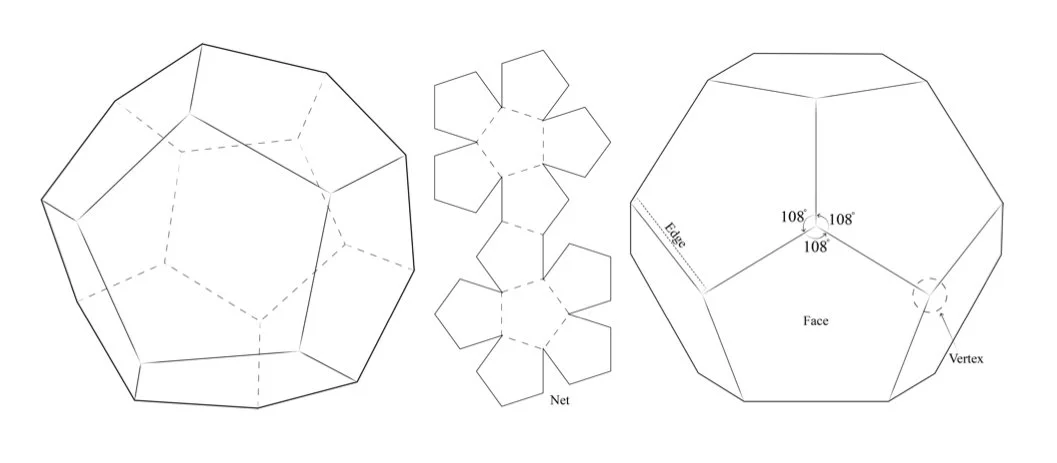
Dodecahedron :
A regular dodecahedron or pentagonal dodecahedron (Fig.29) is a platonic solid that consists of 12 pentagonal faces, which form 30 edges, and 20 vertices. 3 pentagons meet at each vertex, with internal angles of 108 degrees, summing up to 324 degrees (108x3). The dihedral angles are 116.56505 degrees. The dual of the dodecahedron is the icosahedron.
Of the infinite series of 2-d regular polygons, only 3-fold, 4-fold, and 5-fold n-polygons prove useful. Other n-polygons are too ‘round’ to form valid 3-d corners. As seen, this works for 3,4, or 5 triangles, 3 squares, or 3 pentagons around a shared vertex.
Euler provides an elegant formula to distinguish platonic solids from the infinite set of uniform polyhedra. According to Euler, the number of faces ‘F’ added to the number of vertices ‘V’ (corner points), subtracted by the number of edges ‘E’, always equals 2. More simply, F + V - E = 2.
Fig.28
Cube
Fig.29
Dodecahedron
V. THE JITTERBUG AND PLATONIC DIPOLYGONOIDS
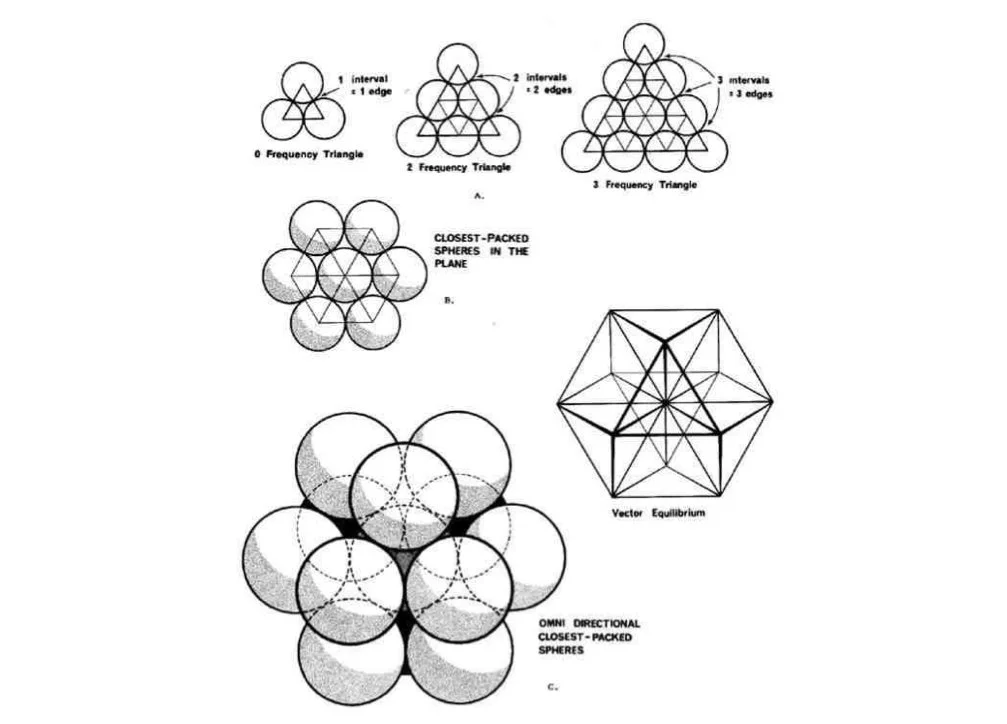
The jitterbug is a set of eight identical regular triangles connected to one another by the vertices (Fig.30). It is a fascinating wireframe tensegrity model which contains the platonic solids within its motion. They can be seen as phases of a dynamic transformation process arising from the close-packing of spheres (Fig.31). These displacive transitions occur when the centre sphere is removed from the close-packing, allowing a series of twist-collapses. The system oscillates, expands, contracts, and folds over tetrahedrons, octahedrons, icosahedrons, to again end with the cubeoctahedron.
Buckminster Fuller describes the jitterbug as ‘the finitely closed, external vector structuring of a vector equilibrium model constructed with 24 struts, each representing the push-pull, action-and- reaction, local compression vectors, all of them cohered tensionally to one another’s ends by flexible joints that carry only tension across themselves, so that the whole system of only-locally-effective compression vectors is comprehensively cohered by omni-embracing continuous four closed hexagonal cycles’ tension.’ Fuller introduced it as an ‘energetic geometry’ which later inspired his rubric of synergetics.
Fig.30
Passing from cubeoctahedron to icosahedron to octahedron and completing the transformation : Fuller with the jitterbug as tetrahedron.
Fig.31
Close packing of spheres
Fuller and Stuart extend his reasoning to create the ‘single-cell jitterbug’ by covering the equilateral triangle faces of the wireframe structure (Fig.32). This led Joseph Clinton to establish similar transformations between some more polyhedra. He added 2 faces to every side of the jitterbug model, thereby making them dipolygons. Adjacent dipolygons are connected with a binary alternating vertex connection system where the top layer of a dipolygon face is connected with the bottom layer of the adjacent dipolygon face. This over-constrains each face and the entire structure to only one angle of rotation. In these stable platonic transformations one can observe jitterbug-like structures appearing while one polyhedron transforms into another. These ‘dipolygonoids’ are able to perform a symmetrical ex- and impansion motion, illustrating a transformation between, for example, the tetrahedron and octahedron (Fig.33).
As Clinton observed in his paper on expanding rigid structures, each triangle is subject to a translation-rotation along its symmetry axis. When starting from the closed position in the tetrahedron, these axes are the four triangular symmetry axes of the tetrahedron. When describing cylinders about the triangles along the axes, each vertex common to two triangles moves along the intersecting curve of the two cylinders.
Both Clinton and Stuart extend the jitterbug transformation by starting this process at other platonic solids (Fig.34, Fig.35) and some archimedean solids too (Fig.36), thus establishing a number of jitterbug-like transformers in which :
Each transformation starts from a platonic or archimedean solid, while certain rotational symmetries of that solid remain.
The transformers are not symmetrical with respect to reflections which leave the solid invariant.
The structures are composed of one or two types of polygons, all having equal edge length.
The motion of the vertices is along the intersecting curve of two circumscribed cylinders.
Fig.32
R. Buckminster Fuller, ‘Single-Cell Jitterbug’
Fig.33
Tetrahedron dipolygonoid expanding into the octahedron through 120 degrees.
Fig.34
Octahedron and cube dipolygonoids : both expanding into the cubeoctahedron
Fig.35
Icosahedron dipolygonoid expanding into the icosadodecahedron through 120 degrees
Fig.36
Cubeoctahedron dipolygonoid further expands into the rhombicubeoctahedron
Fig.37
3-dimensional tessellations : The pyramid and cube modular dipolygonoids both expand into cubeoctahedron-octahedron close-packing.
If one covers the gaps of an expanded dipolygonoid with identical dipolygon modules and connects their vertices with adjacent faces using the same alternating rule, the resulting structure will expand further into another uniform solid. Theoretically one can continue this sequence of expansions to infinity i.e, a spherical dipolygonoid with infinite facets. For example, the octahedron and cube dipolygonoids both expand into the cubeoctahedron (Fig.34). Covering the gaps of these dipolygonoids in their expanded states results in a cubeoctahedron dipolygonoid which will expand further into the rhombicubeoctahedron (Fig.36) which then expands into a snub cube and so on.
One can also construct modular dipolygonoids from all the space-filling tessellations such as the cube lattice, as well as other 3-dimensional modular forms like the pyramid lattice. Coincidentally both these modular jitterbugs expand into a close-packing of the cubeoctahedron-octahedron lattice (Fig.37).
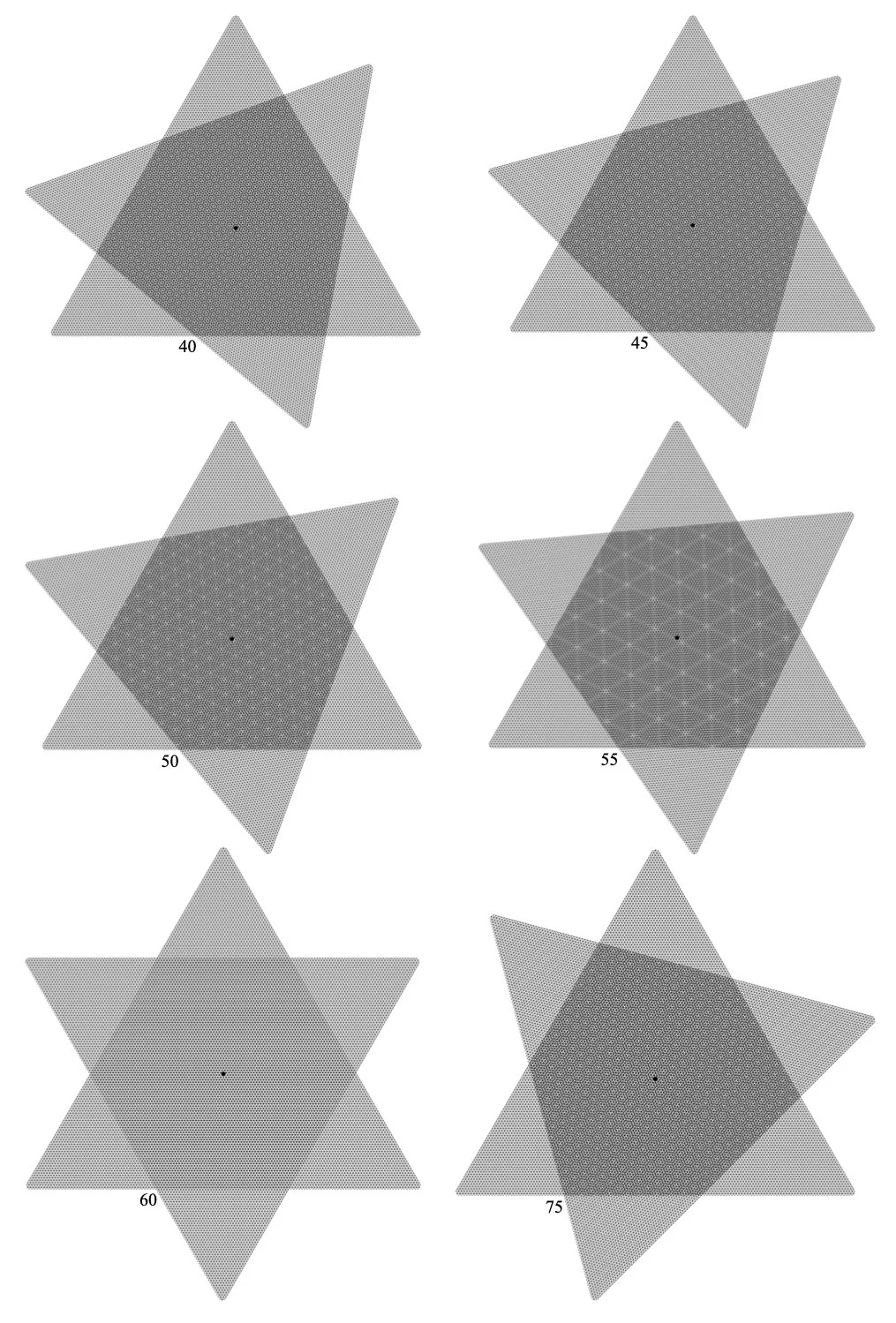
VI. REGULAR NESTED 3-DIMENSIONAL MOIRE PATTERNS
When self-similar transparent grids are applied to each face of a platonic dipolygonoid, the rotation- translation creates a 2- and 3-dimensionally synchronous moire and structural motion.
3-fold dipolygons and equilateral triangle tessellations are used in constructing the tetra-octa-, and icosa- jitterbugs, each with 120 degree periodicity for the 3-fold interference pattern and platonic structure. 4-fold dipolygons and self-similar tessellations are used in constructing the cube, with 90 degree moire periodicity and a 180 degree expansion-contraction cycle. 5-fold pentagons and quasicrystal tessellations are used in constructing dodecahedral jitterbugs, each with 72 degree periodicity and synchronicity.
Since the angle of symmetry of each rotating tessellation is synchronous with the angle of rotational symmetry of the overall structure - and they both exhibit the same n-fold symmetry - the result is a nested, multi-dimensional, regular, and periodic motion and moire pattern. Each platonic dipolygonoid with this self-similar property is perceptually fractal-like in it’s kinematics.
i. Tetrahedral - Moire cell
Moire-cell is the simplest regular 3-dimensional interference pattern (Fig.38). Tetrahedrons consist of 4 identical equilateral triangle faces. All edges are the same length, and its vertices are equidistant from the structure's center. Hence it is 3- dimensionally and geometrically regular, one of five platonic solids. This jitterbug tetrahedron is constructed with 8 equilateral triangles, as there are 2 on each face. It employs an over-constrained spatial mechanism to expand and contract, creating 4 equilateral triangle gaps at 120 degrees of rotation. The resultant structure is an octahedron (8 triangles : 4 faces + 4 gaps), one of the other platonic solids. In a sense the tetrahedron expands into itself as the gaps are identical to the dipolygon faces, illuminating its self-dual property.
Each face has identical wireframe-transparency grids made of equilateral triangles. Rotation causes interference between overlapping grids, creating a ghost-like animation of telescoping equilateral triangles. This moire pattern completes a full cycle at 120 degrees, as does the jitterbug's expansion. Hence moire-cell can be termed regular in the sense it consists of only equilateral triangles (the structure, grid, and interference), with 120 degree rotational periods in 2-d interference and 3-d structure.
As the faces rotate oppositely, the triangular pattern zooms in, and at 30 degrees of rotational expansion of the model, the animation magnifies into its most intricate dance. It zooms back out at 60 degrees, where the ghost pattern disappears as the grids overlap. This sub-period repeats for another 60 degree loop where the pattern is inverted, till the tetrahedral cell is fully expanded into an octahedron, or each equilateral triangle reaches 120 degrees of rotation vis a vis it’s face counterpart. One can observe the central triangle in the moire animation point upwards at 59 degrees but downwards at 62 degrees of rotation of the grids, illustrating this sub-period inversion. Since moire-cell is self-dual and its expansion leads to 4 triangular gaps, the 3-fold wireframe grid and interference are further appropriate.
The physical model is made of transparent 1mm thick acrylic sheets with graphic sticker- transparencies (Fig.39). Stickers are stuck on opposite sides of the two sheets on each face to prevent scratching of the patterns through wear and tear. The 1mm thickness of the sheets is enough for the moire pattern to be apparent and thicker sheets further limit the structure’s expansion and contraction. Each dipolygon unit is connected with stainless steel rivets at the center, and by stainless steel rings at the vertices. Since its completely interconnected, one can expand the model by squeezing two adjacent vertices towards one-another, or with a chain that can be lifted to allow gravity to open the structure.
Fig.38
Moire-cell : The simplest regular 3-dimensional interference pattern with 120 degree periodicity
Fig.39
Moire-cell : physical construction and transformation through 120 degrees
ii. Octahedral - Moire diamond
Moire-diamond is the second regular 3- dimensional interference pattern. Octahedrons consist of 8 identical equilateral triangle faces. All edges are the same length, and its vertices are equidistant from the structure's center. Hence it is 3-dimensionally and geometrically regular, the second of five platonic solids. The jitterbug octahedron is constructed with 16 equilateral triangles, as there are 2 on each face. It employs an over-constrained spatial mechanism to expand, creating 6 square gaps at 120 degrees of rotation. The resultant structure is the cubeoctahedron (8 triangular faces + 6 square gaps), one of the archimedean solids. This kinematic shows us the cube is dual to the octahedron.
If one superimposes wireframe 3-fold grids, the 2- and 3-dimensional interference and structural periodicities would be synchronous at 120 degrees, as is with the tetrahedral moire-cell and icosahedral moire-jewel (Fig.38, Fig.39, Fig.41).
Since this octahedral-diamond transforms into a cubeoctahedron causing 6 square gaps to emerge, the 3-fold alternately checkered grids (black and transparent triangles, where the two layers have alternate colour arrangements) and their square ghost animation create an appropriate superimposition for the dipolygon modules.
In this case the 2-d perceptual moire and 3-d structural gaps caused by nested 3-fold rotations are 4-fold, with the interference requiring 360 degrees to complete one period of symmetric rotation (Fig.21).
The physical model (Fig.40) is opaque when fully closed because the black triangles of the two grid layers alternately overlap on every face. One cannot observe the full moire pattern because the structure only expands and contracts through 240 degrees. A chiral octahedral transformation (Fig.48) allows two full periods of the 360 degree checkered interference within its structural cycle of 720 degrees.
Fig.40
Moire-diamond : physical construction and transformation through 240 degrees
iii. Icosahedral - Moire jewel
Moire-jewel is the third regular 3-dimensional interference pattern. Icosahedrons consist of 20 identical equilateral triangle faces. All edges are the same length, and its vertices are equidistant from the structure's center. Hence it is 3- dimensionally and geometrically regular, the third of five platonic solids. This jitterbug icosahedron is constructed with 40 equilateral triangles - 2 on each face. It employs an over-constrained spatial mechanism to expand, creating 12 pentagonal gaps at 120 degrees of rotation (Fig.35). The resultant structure is the icosadodecahedron (20 triangular faces + 12 pentagon gaps), an archimedean solid. This kinematic expansion shows us the dodecahedron is dual to the icosahedron.
If one uses wireframe 3-fold grids, the 2- and 3- dimensional interference and structural periodicities would be synchronous at 120 degrees, as is with the tetrahedral moire-cell and octahedral moire-diamond. In Fig.41 moire jewel expands and contracts through 240 degrees, as seen from an orthographic perspective with a vertex-view of the icosahedron.
Fig.41
Moire-jewel : A regular 3-dimensional interference pattern with 120 degree periodicity
iv. Hexahedral - Moire box
The regular 4-fold period cycle is a nested 2- and 3-dimensional symmetry of squares. Cubes consist of 6 identical square faces. All edges are the same length and its vertices are equidistant from the structure's center. Hence it is 3-dimensionally and geometrically regular, the fourth of five Platonic solids. This jitterbug cube has 12 squares, two on each of the six faces. A dipolygonoid kinematic mechanism allows the cube to expand, creating 8 equilateral triangle gaps at 90 degrees of rotation. The resultant geometry, a cubeoctahedron (6 square faces + 8 equilateral triangle gaps), is a semi-regular archimedean solid, and this kinematic shows us the octahedron is dual to the cube.
When in motion, the rotational interference of overlapping self-similar 4-fold wireframe grids creates a ghost-like animation of telescoping squares with a periodicity of 90 degrees (Fig.42).
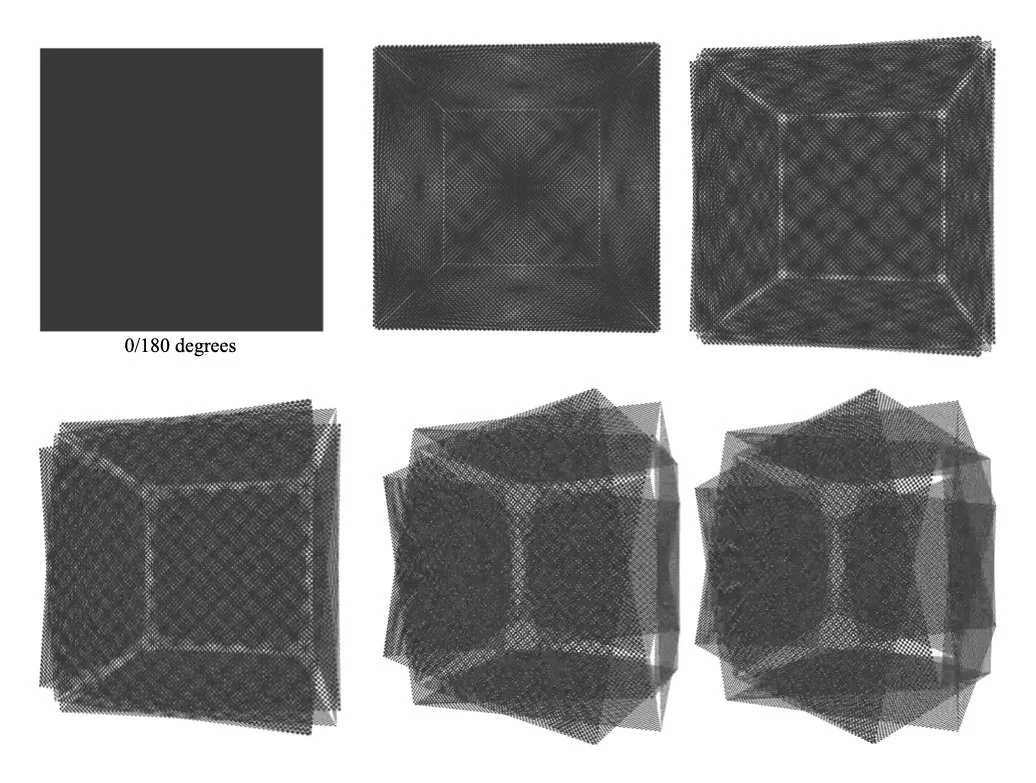
Checkered-transparency grids - where the outer and inner layer have alternate combinations of black and transparent squares - completes a cycle i.e, 1 period, at 180 degrees. The jitterbug also completes an expansion-contraction cycle in 180 degrees. When seen head on, an opaque black square is visible if the structure is fully contracted (Fig.43, Fig.44). Moire-box is thus regular because the structure, grids, and interference are all squares, with a periodic interval of 90 or 180 degrees in interference and structure.
Fig.42
Moire-box : physical construction and transformation through 180 degrees, with 90 degree periodicity
Fig.43
Moire-box : Alternate checkered 4-fold grids on a cube dipolygonoid through 90 degree transformation, and a symmetrical periodicity of 180 degrees
Since 2-dimensional moire patterns require tessellations i.e, two identical grids of regular polygons, one can use the space-filling property of cubes to create a 3-dimensionally modular and nested tessellation-symmetry as well. In a sense this would be a truer 3-dimensional moire than a single unit of the moire box. By superimposing 4-fold wireframe or checkered grids on a cube lattice dipolygonoid as seen in Fig.37, this is achieved. Similarly, the triangular pyramid lattice that’s seen in Fig.37 can be made transparent and superimposed with 3-fold graphic-sticker grids, creating a nested and modular 3-dimensional 3-fold interference pattern. We can maintain the regularity of an octahedral symmetry in this case by using 2 such pyramids - one on top of the other, with the bottom inverted. These ‘modular-moires’ can be made chiral as well (Fig.50, Fig.53).
Fig.44
Moire-box : Physical construction of alternate checkered 4-fold grids on a cube dipolygonoid, with a periodicity of 180 degrees
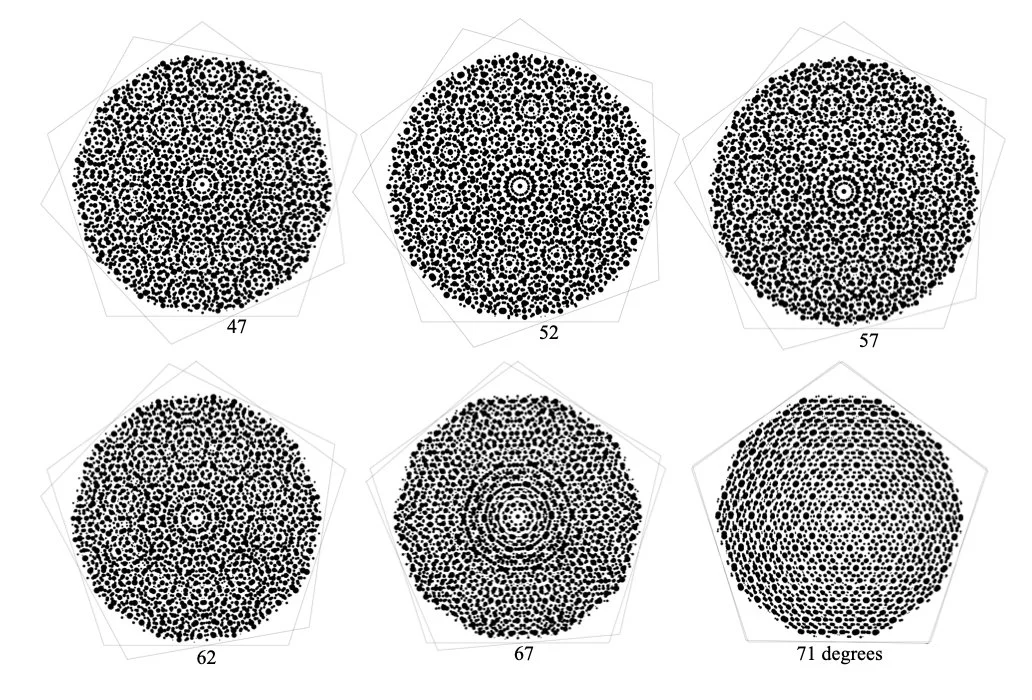
v. Dodecahedral - Quasi-cells
3-dimensional 5-fold quasi-cells with pentagonal symmetry have 72 degree moire periodicity and a 144 degree structural rotation. I have superimposed and rotated identical quasicrystal patterns on each face of a physical dodecahedron transformer to create circular dot interferences embedded in their geometries, revealed through the kinetic motion of the sculpture (Fig.45).
This dodecahedron kinetic transformer was a fitting backdrop to these rotational experiments since it’s made of 12 pentagons, which also exhibit 5-fold symmetry. When the structure expands, the 20 triangular gaps together make an icosahedron (dual to the dodecahedron), which adds up to form a gorgeous icosadodecahedron.
I’ve used 5-fold Penrose tiling, Shechtman’s 10-fold X-ray diffraction image of the molecular structure of Al86Mn14 (aluminium manganese), an icosahedral quasi-symmetry, and 2 more molecular lattice symmetries that are 8- and 12-fold. The dodecahedron is a meaningful kinetic backdrop for these projections and their beautiful rotational dances.
Fig.45
Quasi-cell: Physical transformation of an 8-fold quasicrystal pattern on a dodecahedron dipolygonoid
VII. CHIRAL TRANSFORMATIONS
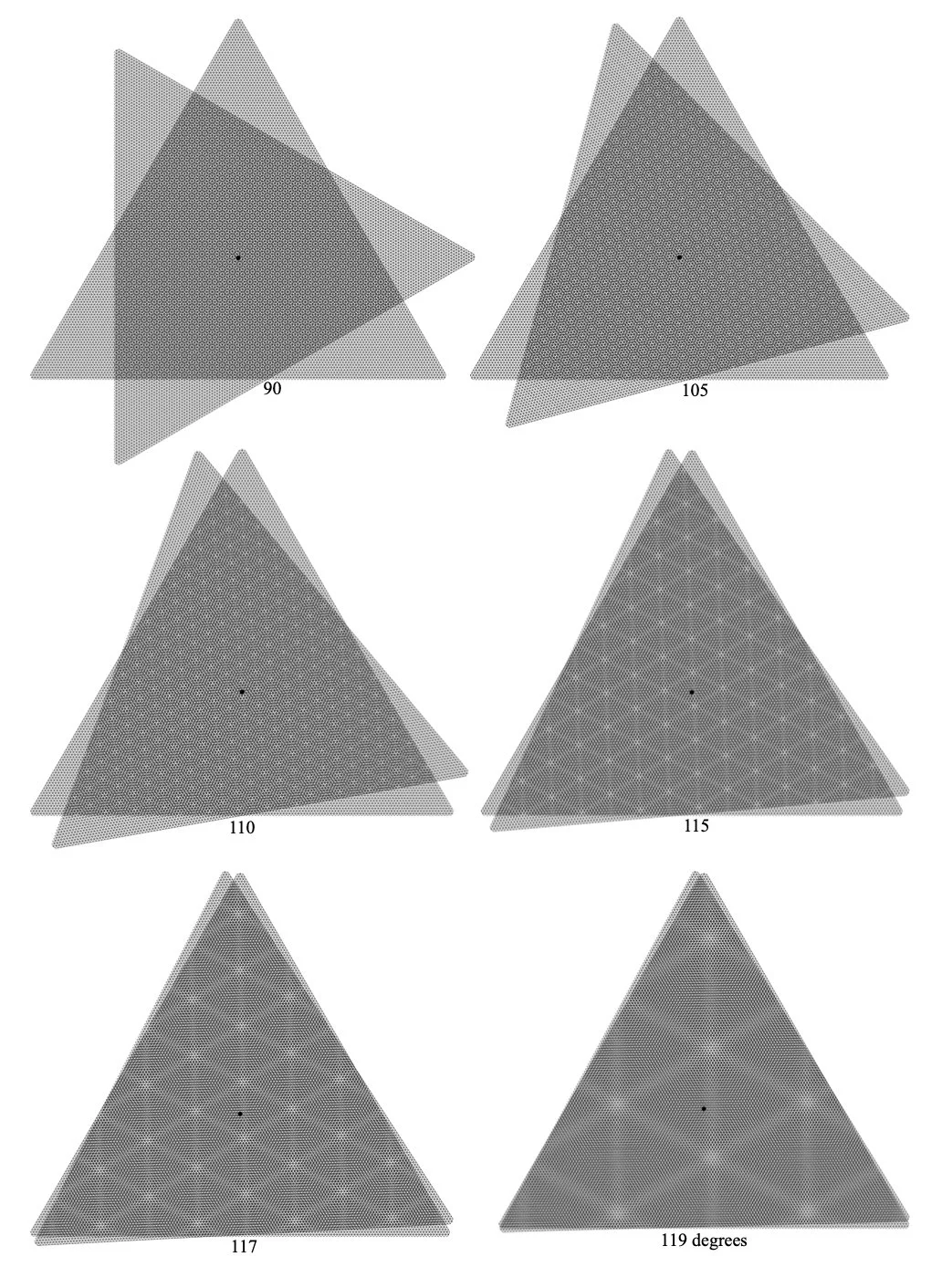
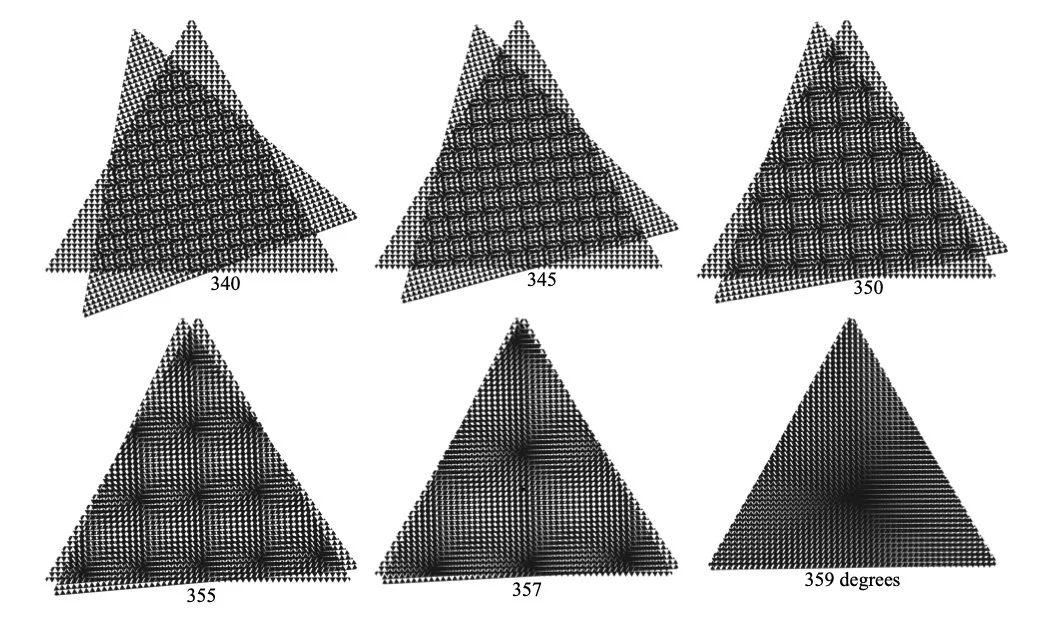
In a sense a true 3-dimensional moire pattern would require a 360 chiral transformation where each face passes through the center of the platonic jitterbug and the dipolygons turn inside-out or invert, creating a 720 degree structural cycle.
Dipolygon modules have 2 layers. One of these layers rotates clockwise while the other rotates counter-clockwise. This gives chirality to dipolygonoid transformations. In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone.
The physical dipolygonoids are limited in their expansions by the connection system, allowing motion up to one translation. Once the structure is fully expanded, it can only be contracted by a symmetrical rotation in the opposite direction of the expansion.
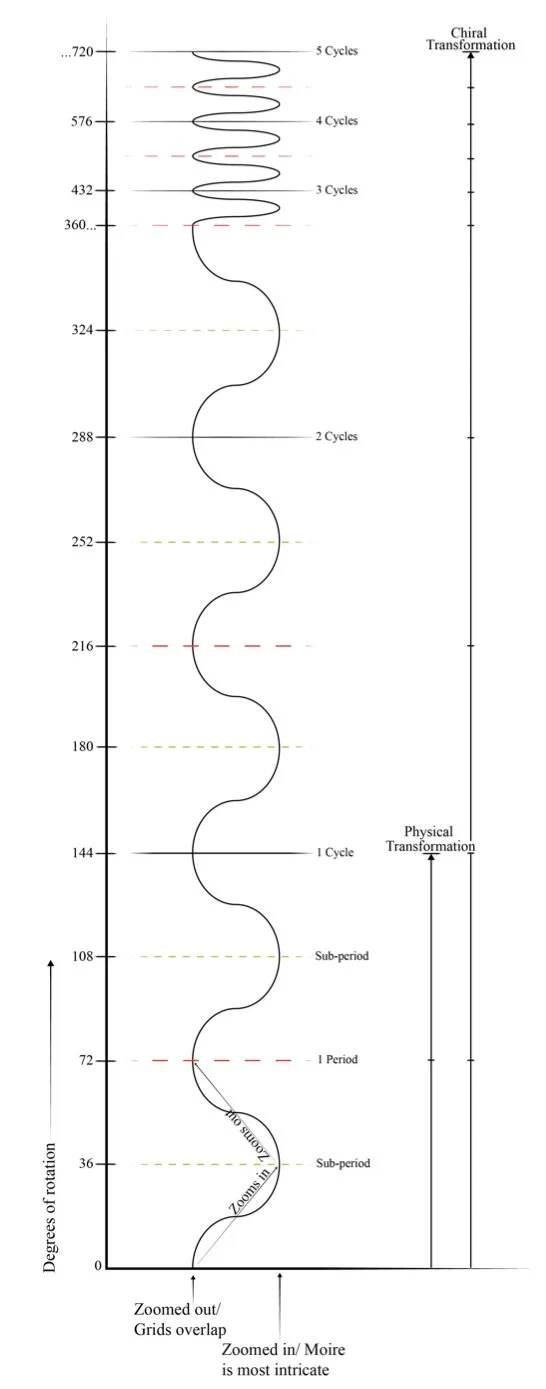
In the mathematical realm, chiral transformations can continue through a 720 degree rotation for all the platonic dipolygonoids, where the opposite dipolygon faces pass through each other, becoming congruent in the process. This was first observed by Joseph Clinton. Each group of rotations has a point of invariancy O, being the one point of intersection of all axes of these rotations. Chiral structures invert after each dipolygon face passes through this center O. It is an interesting ‘double-duality’ as the moire patterns (that have 2 sub-periods within each periodic interval) also invert after 1 sub-period.
In this paper, regular polygons have been defined by a rotation around a point O. The advantage here is the consistency in generating higher groups of rotational symmetries. For example, a 3-dimensional chiral transformation goes through a 720 degree rotation, with all faces passing through the point of invariancy O, and each dipolygon module is rotated about the center of it’s face, O. This creates a truer 3-dimensional interference as it is a symmetrical rotation of regular polygons and platonic jitterbugs. Here a symmetrical rotation cycle is defined as a transformation which preserves the shape and position of an object.
In the case of the cube, the axis of rotation in 2-dimensions is through the center of it’s squares O, which are 1-dimensional points on a plane where each dipolygon face is conjoined (Fig.5). The center of rotation in 3-dimensions is the intersection of the cube’s symmetry axes, O, a point of invariancy in space. Later, we will extend this reasoning into higher dimensions as well.
Adrian Rossiter has created boolean-like visuals for these chiral polyhedra. One has to imagine superimposing wireframe grids and their moire patterns from previous figures to Rossiter’s models, to truly visualise 3-dimensionally symmetric and periodic moire patterns.
The sine wave of moire periodicity, and structural rotation-translation cycle for the 3-fold, triangle-based self-similar structures are shown in Fig.46. One can also observe the tetrahedral, octahedral, icosahedral, and octahedra-tetrahedra lattice’s chiral transformations through 720 degrees (Fig.47, Fig.48, Fig.49, Fig.50).
In Fig.47 we see the tetrahedral jitterbug begin at the expanded octahedron state, from where it contracts through the tetrahedron and stellated octahedron phases with orange 3-fold polygons on the top layer of each dipolygon face. As these faces pass through the center-point of invariancy O of the form the structure inverts as the blue polygons are now on top (on the exterior) of each dipolygon module. From here it unfolds and expands into a blue stellated octahedron, tetrahedron, and octahedron, then reverses and passes through O again, reverting to the orange-exterior, and continues through the orange stellated octahedron and tetrahedron phases to end with a symmetrical 720-degree rotation cycle in the original octahedral position. This structural inversion occurs in all chiral transformations.
If we superimpose transparent wireframe 3-fold grids on self-similar 3-fold dipolygon faces of this tetrahedral chiral transformation, we create self-similar moire patterns of equilateral triangles with six 2-dimensional moire-periods within one 3-dimensional chiral cycle (Fig.46). The interference and structure invert halfway through their periodicities and cycle, revealing their duality. This is true for the tetrahedral, octahedral, icosahedral, and octahedra-tetrahedra lattice arrangements in their chiral moire forms.
Superimposing self-similar 4-fold grids on the 4-polygons of a chiral cube would create 4-fold moire patterns with 90 degree periodicity, thereby having eight 2-dimensional moire-period intervals within one 720-degree 3-dimensional chiral cycle (Fig.51, Fig.52), or 2 periods within one physical cube dipolygonoid expansion-and-contraction (Fig.42). The same is true for the 3-d cube lattice (Fig.53). Checkered 4-fold grids have four 180-degree periods in a chiral cycle. The chiral dodecahedron superimposed with 5-fold aperiodic patterns such as Penrose tiling have moire periodicity of 72 degrees, with ten 2-d periods within one 3-d 720-degree structural cycle (Fig.54, Fig.55). In Fig.56 we see the sine wave periodicity and structural cycle of every platonic jitterbug.
Fig.46
Sine wave form of moire pattern, and structural transformations : in wireframe 3-fold moire-cells, moire-diamonds, moire-jewels, and octahedra-tetrahedra lattice
Fig.47
360 degree chiral transformation of the tetrahedron through 720 degrees of rotation
Fig.48
360 degree chiral transformation of the octahedron through 720 degrees of rotation
Fig.49
360 degree chiral transformation of the icosahedron through 720 degrees of rotation
Fig.50
360 degree chiral transformation of the octahedra-tetrahedra lattice through 720 degrees of rotation
Fig.51
Sine wave form of moire pattern, and structural transformations : in wireframe 4-fold moire-box and moire-box lattice with 90 degree periodicity
Fig.52
360 degree chiral transformation of the cube through 720 degrees of rotation
Fig.53
360 degree chiral transformation of the cube lattice through 720 degrees of rotation
Fig.54
Sine wave form of moire pattern, and structural transformations : in 5-fold quasi-interferences and their self-similar dodecahedral jitterbug with 72 degree periodicity
Fig.55
360 degree chiral transformation of the dodecahedron through 720 degrees of rotation
Fig.56
Sine wave forms and periodicity of all five platonic jitterbugs with self-similar moire patterns, through 720 degree chiral rotations
VIII. REGULAR POLYTOPES BY DIMENSION
A 0-dimensional shape is a single point in space, or on a plane. Hence there is only one regular shape in the 0th dimension, a point.
In 1-dimension, we may extend this point-like shape into a straight line of any length, hence there is also only one regular shape in 1-dimension, the straight line.
We’ve discussed the infinite 2-dimensional series of regular polygons constructed with lines, which extends to a circle at infinity, as well as the five Platonic solids that exhibit regularity in 3-dimensions.
Just as a series of conjoined points from the 0th dimension make a 1-dimensional line, and equilateral-equiangular congruent lines create the regular polygons in 2-dimensions, of which three are able to construct the five regular polyhedra in 3-dimensions, i.e, 3-, 4-, and 5-gons, we may use this reasoning to surmise regular shapes in n-dimensions.
As Carlo H. Sequin points out, there are six regular 4-dimensional polytopes that can be constructed using 3-dimensional polyhedra. Each shape is constructed with only one type of regular 3-dimensional polyhedron as a crust or surface, where all corners and edges between these ‘cells’ are the same. For example, we construct cubes out of squares by sweeping out their volume, so we make a hypercube out of cubes on its surface, around a shared corner. The tetrahedron, octahedron, cube, and dodecahedron all translate into 4-dimensional regular polytopes, but the icosahedron does not because it has a very shallow dihedral angle of 138~ degrees, not allowing for a valid shared corner. The tetrahedron can be extended into three regular 4-dimensional shapes, whereas the octahedron, cube, and dodecahedron extend into only one regular 4-dimensional polytope each :
Tetrahedral :
Simplex or 5-Cell - 3 tetrahedra around a shared edge.
Cross polytope or 16-cell - 4 tetrahedra around a corner. Dual to the hypercube.
Tetraplex or 600-Cell - 600 tetrahedra with 20 meeting at each vertex, hence it is the 4-dimensional analogue of the icosahedron. Dual to the 120-cell.
Hexahedral :
Tesseract or Hypercube or 8-cell - 8 cubes with 3 around a shared edge. It has 16 vertices, 32 edges, and 24 faces.
Octahedral :
Octaplex or 24-cell - 24 octahedra with 3 octahedra around a shared edge, 6 around a shared vertex.
Dodecahedral :
Dodecaplex or 120-cell - Made of 120 dodecahedra in a thick crust, with 4 meeting at each vertex.
For regular 5-dimensional polytopes, we use regular 4-dimensional polytopes that have dihedral angles such that a set of them can fit around a shared edge to make a valid corner. Most are too round (as they have shallow dihedral angles) to create higher dimensional polytopes. Only the tetrahedral, octahedral, and hexahedral 4-dimensional polytopes i.e, the simplex (5-cell), hypercube (8 cell), and the octaplex (24-cell), translate to n-dimensional polytopes. Therefore there are only 3 regular polytopes in any dimension higher than 4-dimensions.
First is the simplex series, where by adding a tetrahedral vertex at the center of the n-dimensional simplex’s gravity raises a new vertex that is equidistant from the n -1 dimensional simplex’s vertices.
The second set that works for all higher dimensions is the hypercube series (Fig.57). They are the equivalent of the cube in higher dimensions, with which we measure 3-dimensional space, just as we use squares to measure 2-dimensional space and 8-cells 4-dimensional space. This occurs by stepwise extrusions. Squares when extruded perpendicular to themselves create cubes, cubes extruded perpendicular to themselves create the tesseract, hypercubes extruded perpendicular to themselves creating 5-dimensional measure polytopes, and onwards and upwards - an infinite series.
The third series is the octahedral cross-polytope series - dual to the measure polytopes - constructed using 24-cells. Every n-dimensional cross polytope is made out of cross-polytopes of n -1 dimensions. By replacing each 24-cell with a vertex at its center, when connected properly, creates the n +1 dimensional polytope analogue.
Thus, the sequence of regular shapes by dimension is 1, 1, infinite, 5, 6, 3, 3, 3, 3, 3,…., for the 0th, 1st, 2nd, 3rd, 4th, 5th, 6th, 7th, 8th, 9th,…. dimension.
Fig.57
Regular shapes in dimensions 0 to 5. Hypercube series : a point, line, square, cube, tesseract, and measure polytope
IX. HIGHER DIMENSIONAL KINEMATICS
When we consider n-dimensional geometries such as regular polytopes or honeycomb lattices, many questions arise. Firstly, the 3-dimensionally synchronous platonic-moire structures in chiral form can translate into their 4-dimensional regular analogues. Just as we rotate 3-d dipolygonoids out of 2-d dipolygons on each side, we can revolve 4-d dipolytopes out of 3-d dipolygonoids on their crust or surface.
A simplex (Fig.58), cross polytope (Fig.58), or tetraplex (Fig.58) can have two layers - a dipolygon - on every 3-fold face of its exterior and interior tetrahedra. When superimposed with wireframe 3-fold grids, a self-similar 3-fold interference is created on every face of every dipolygonoid as the 3-fold 4-dimensional dipolytope rotates through a symmetric multi-dimensional transformation. The same applies for the 3-fold octaplex and its octahedra (Fig.58), the 4-fold tesseract and its cubes (Fig.58), and the 5-fold dodecaplex and its dodecahedra - seen here from an interior view (Fig.58).
Three of these polytopes - the simplex, octaplex, and tesseract can have chiral forms in 5-dimensions, and in all higher dimensions as well. Only the tesseract honeycomb creates a valid modular higher-dimensional lattice, but one can create an octaplex-tetraplex honeycomb or 5-dimensional quasi-crystalline lattices that are chiral and periodic as well.
In each case, the center point O of each face is the centre of each 2-d dipolygon rotation, the spatial center point O of the 3-d chiral structure is the point of invariancy about which the chiral dipolygonoid expands and contracts (along the intersection of all dipolygon axes), and these dihedral axes are the tensor-lines of invariancy O — O1, equidistant from every platonic vertex in the 4-d dipolytope transformation about which the polyhedra revolve.
Carlo Sequin points out that one gets a better understanding of polyhedra and polytopes by using wireframe models exclusively. For example, by looking at the convex hull of a 3-dimensional cube, we can infer what is happening on the backside. But by the time one visits a tesseract - a 4-dimensional hypercube - filling in faces with grids and moire patterns blocks part of the information, making it difficult to visualise. Wireframe models allow one to see into and through to the backside of these objects, and one can use perspective projections to create nested 3-dimensional models.
Now given the concept of combining different shapes that intersect with one-another to form a moire pattern, rather than having 3-dimensional elements and somehow overlap them, we can go in the other direction and use 1-dimensional elements. We can create higher-dimensional polytopes - intersecting and overlapping in their wireframe mode - rotating against one another. What we’re looking at is the patterns generated by the wireframes of these objects, which would have a moire-like effect.
Sequin thus observes the simplest 4-dimensional moire pattern starts out as a 1-dimensional wireframe element. We use two identical elements - polytopes in their wireframe mode - that are perfectly overlapping each other. We start along any one particular axis and rotate the two elements against one another. Some of the edges will split and drift apart to create new interesting patterns. In a sense this is the simplest moire module for any regular 4-d dipolytope.
If we are to maintain the 3-fold symmetry of the tetrahedron and 3-polygon, we can rotate 3 identical simplexes about a common axis or multiple axes, instead of 2. Thus one can build regular 4- and 5-dimensional interference models for all the 4-d and 5-d polytopes and observe their Boolean intersections and projection moire patterns.
In the case of the simplex, the axes of rotation are the four axial vertices of a 3-dimensional tetrahedron that remain invariant through the 4-dimensional transformation, and a simplex’s equidistant vertex extruded into an edge-axis in 4-dimensional space remains gravitationally invariant through the 5-dimensional transformation. One continues this reasoning by creating raised, gravitationally locked, and rotationally invariant corners in the n-1 dimensional polytope about which the n-dimensional models symmetrically revolve.
Higher-dimensional kinematics, let alone chiral moire-polytopes, are difficult to visualise. Perspective projections (Fig.58) are used to show the 6 regular 4-dimensional polytopes, and in Fig.59 we see a stepwise extrusion that leads to an oblique projection of a 6-dimensional measure polytope. This is achieved by sweeping out the edges and vertices of a cube in the 3 higher dimensions, where every edge is a sweep-path of one of its cubes.
Lastly, one can describe platonic polytopes and their 3-dimensional chiral analogues as Fourier transforms and assign eigenvalues to each symmetrical transformation.
Fig.58
Six regular polytopes in 4-dimensions
Fig.59
6-dimensional measure polytope : oblique projection